作者简介: Ent (古生物学博士生，科学松鼠会成员)

昨天，一篇来自浙江大学、浙江工商大学和中科院理论物理研究所的论文公布在了预印本网站上。根据媒体的宣传，研究者 “找到了石头·剪刀·布的制胜策略”。

自然而然地，很多网友的反应是：“这还需要你研究？”

网友评论截图 - 图片来源：凤凰网

但是只需扫一眼就会发现，研究者不幸又被标题党坑了。他们寻找的不是怎样玩赢剪子包袱锤，而是通过人们在剪子包袱锤里的行为来判断哪一种理论更能预测人类——是传统博弈论的纳什均衡，还是演化博弈论。

因此，我打算从我熟悉的演化博弈论角度来越俎代庖，尝试解读这项研究为什么不是在浪费钱。

为了帮助理解它，我会讲四个故事。这四个故事从易到难，如果你已经对这个领域很熟悉了，可以跳过前面的几个故事。

第一个故事: 囚徒困境

一个有钱人被发现死于家中。警方抓获了两个犯罪嫌疑人并查获了赃物，但两人辩称说他们只是小偷，进屋时那个人已经死了。没有更多证据，调查陷入僵局。

于是警方把两人分开，分别对他们说:

如果你俩都不认罪，我只能判你盗窃，一年了事；如果你招了他没招，你算作立功，不用坐牢，而他得十五年。如果如果他招了你没招，那反过来。但如果他和你都认了，谋杀罪每人十年。

嫌疑人 X 心想: 如果 Y 不招，那么我也不招的话会判一年，我招了无罪释放。招了更划算。

而如果 Y 招了，那我不招的话十五年，招了只有十年。还是招了更划算。

显然我应该招啊。

而嫌疑人 Y 当然也是这么想的。结果，两人都判了十年。任何一人改策略都只会让自己处境更糟，这便是一个纳什均衡。

可是，如果从整体上看，最好的结果显然是两人都不招，各判一年。双方都是理性考虑谋求自己的最大利益，结果却是两人都遭遇了坏场景；无论是整体最好场景 (各判一年) 还是个人最好场景 (直接释放) 都不可能发生。这就是为何囚徒困境是个“困境”。每个人都很精明，最后怎么弄了这么个烂摊子？

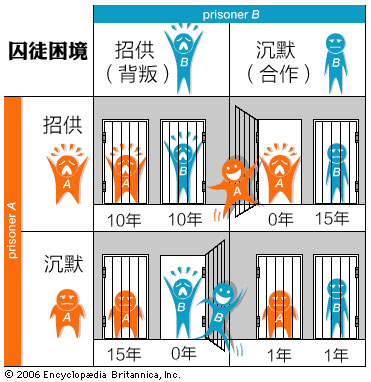
囚徒困境示意图 (或者，“收益矩阵”) - 图片来源: Encyclopaedia Britannica

按照囚徒困境术语，不招的行为算作“合作” (和你的狱友合作，不是和警方合作)，而招认的行为算作“背叛”。双方都合作最好，双方都背叛则两败俱伤。按照这个故事，合作根本不可能出现啊。

现实中类似囚徒困境的场景常常出现。但是，更多的结局似乎是合作，而不是背叛。为什么？

可能的原因是，困境不止这一次。

第二个故事: 重复囚徒博弈

如果嫌疑人 X 和 Y 是陌生人，那么两人的下场都是十年。但是他们也许是两肋插刀的好哥们，或者有血亲，或者属于同一个组织——总而言之，用博弈论的术语，他们以前也许打过交道，将来还很可能继续打交道。这时，“合作”就不是什么难以想象的事情了吧。

因此，一位名叫罗伯特·阿克斯罗德的政治学家在上世纪 80 年代初做了一个名垂青史的实验。他在计算机里摆了一场锦标赛，有很多名虚拟的参赛选手，双方捉对厮杀——哦不，是捉对进行重复囚徒博弈。按照博弈的结果记分，你背叛他合作，则你得 5 分他得 0 分，双方都合作各得 3 分，双方都背叛各得 1 分。

然后，他向全世界征集策略，每一个得到的策略变成一个参赛选手。提交的策略共有 14 个，来自经济学、社会学、政治学和数学等等领域，再加上一个“完全随机”的对照策略，共 15 “人”进行比赛。这里面有些策略极其复杂极其精妙，比如有一个策略用马尔科夫过程为对方的行为建立模型，然后用贝叶斯推断最好的选择。

但是，最后得分最高的竟然是所有提交策略里最简单的一个——“一报还一报” (TFT, tit for tat)。这个策略一共只有两条规则: (1) 第一步先合作，(2) 从第二步开始，对方上一轮出的是什么，我就出什么。提交这个策略的是维也纳的安纳托·拉伯波特，他写这个策略只用了 4 行 BASIC 代码。

阿克斯罗德发表了锦标赛的分析结果，并邀请大家吸取经验教训提交新一轮策略——这次他获得了 62 个策略，不但有上面提到的领域，还包括了演化生物学、物理学和计算科学等新学科。只有一个人厚颜无耻地原样提交了上次的卫冕冠军，那就是拉伯波特本人。你猜对了。他又一次获得了胜利。

TFT 这个“报仇者”成功的秘诀并不复杂。阿克斯罗德说，它有三个要素: 它第一轮总是合作，先表示善意；它会惩罚背叛者；如果对方改过自新，它也不会咬住不放。

但是甘地说过: “以眼还眼，举世皆盲。” 现实中总会因为各种原因结下仇怨，但我们也没有从此冤冤相报何时了。这又是为什么？

可能是因为，现实本来也和阿克斯罗德的模型有些重大差别。

第三个故事: 有突变和自然选择的重复囚徒博弈

(1) 自然发现了宽恕

阿克斯罗德锦标赛有两个重大缺陷。

其一，双方的行为都是完美的，没有误会，没有失误，哪怕不知道对方想什么，至少知道对方做了什么。但现实里多少悲剧源于双方一开始的误会啊！这个重要因素显然不该忽略。

其二，每一个策略的“环境”都是武断决定的。一个策略能否成功，和它身边别的策略如何有很大的关系。假如群体里全都是永远背叛者，那么报仇者完全占不到任何便宜。而阿克斯罗德锦标赛里的参赛选手都是人为提交的，这可不能说是有代表性的样本。

因此，在阿克斯罗德实验的基础上，马丁·诺瓦克制定了一轮新的锦标赛: 引入了自然选择。

他不再邀请人类专家设计策略，而是规定了一个大小合适的策略空间，允许策略在里面进行“繁殖”和“突变”。每一轮得分高的策略后代多，得分低的没有后代甚至自己都消失掉，但每个后代的策略也都和自己有十分微小的差异。此外，每次行为都有一定的“误会”概率——本来我应该合作，但实际出手的却是背叛。

一开始，故事的发展和上面一样。起始的一团糟很快被谁都不信任、每一局都背叛的“背叛者”横扫，但其中很快又出现了一小团一报还一报的“报仇者”。然后报仇者有很大的概率靠自己内部合作，反过来推倒背叛者。

但是现在故事不会到此结束了。因为有误会。

报仇者很擅长对付坏人。但是如果对方不是坏人，而是犯了错误的好人呢？报仇者太记仇，不会放过这一点，如果对方也是报仇者，那相互合作立刻会变成相互背叛，就要陷入冤冤相报何时了的永远循环之中了。

这时，突变出现了“宽恕者”。它的策略学名叫“慷慨的一报还一报 (GTFT)”。它的特点是，即使对方出了背叛，下一轮也有一定的概率选择合作，这样就可以挽救陷入无穷背叛的可能。在论文里，诺瓦克骄傲地宣布: “自然选择发现了宽恕”。

显然，宽恕存在的前提是周围有足够多的好人 (报仇者或者其他宽恕者)。如果周围都是坏蛋 (背叛者)，你的宽恕只会被别人利用。

可好人太多了，又会有另一个问题。

(2) 历史的循环

如果周围都是好人，大家其乐融融，那么最好别坏了人家心情，干脆做个滥好人得了！不管怎么样我都永远合作。这比报仇者和宽恕者对误会的忍受能力更强，宽恕者还有一定概率不原谅，滥好人则是永远原谅，立刻拉回合作的“正轨”，所以它的得分更高。这整个群体会逐渐变成都是滥好人——

但是，坏人从未远去。群体里永远会因为突变而出现新的坏人。而一群只知道合作的滥好人，面对坏蛋那就是白花花的肥肉啊。很快无比成功的坏人会占据群体的大部分。

于是，一切重新开始。

这个坏人->报仇者->宽恕者->滥好人->回到坏人的循环是极其普遍的，而且它的普遍不止存在于博弈论模型里——好人合作打败了坏人，多年以后好人放松了警惕、坏人于是东山再起，这个叙事模型在各种故事传说里都十分普遍。至于这能否作为现实人类历史上战争和平循环的抽象表述，那就见仁见智了。

(3) 打破轮回？

那么，我们注定只能面对这个无尽循环了吗？并非如此。诺瓦克的初代模型里，每个策略只能考虑上一轮对方出了什么。如果它不但考虑了对方，还考虑了自己呢？如果它关注的不是对方的策略，而是策略带来的结果呢？

在改进之后的模型里，意外出现了一个新的稳定策略: “输则改之，赢则加勉 (WSLS, win-stay, lose-shift)”。

这策略很简单。如果我上一轮占了便宜 (双方都合作，或者他合作了我背叛)，那这一轮我继续上轮策略。如果我上一轮吃了亏 (双方都背叛，或者我合作了他背叛)，那这一轮我就换一种策略。换言之，这是一种“反思”型。

当两个反思者相遇，它们大部分时间都合作。万一遭遇了噪音，那么下一轮双方都背叛；再下一轮双方又合作了。纠错延迟只有1回合。这一点比宽恕者更强，只比滥好人弱一点点。

但反思者不怕滥好人。和滥好人打交道，开始双方都合作，但是早晚要出现误会导致反思者背叛，接下来……反思者发现滥好人不懂得报复。于是以后每一轮都是反思者背叛、滥好人合作，没有分辨力的后者遭到惨无人道的剥削而退出游戏。这样一个反思者组成的社会不会随着时间推移而“放松警惕”变成滥好人，当然也就不会遭受坏蛋的后续必然入侵。

等一下，这“反思”策略——不就是报道里说的，石头剪刀布的制胜策略？

没错，石头剪刀布不是囚徒困境。但是，故事还没完。

第四个故事: 关于人类

诺瓦克的本行可以算作是演化生物学家。他们关心的，是在一个自然选择的框架下，合作何以可能。这个框架认为，虽然动物的智力各不相同，但自然选择会将策略植入它们的大脑中。好的策略自然能流传，哪怕动物本身不理解这个策略为何好、甚至不知道自己正在执行一个策略。自然选择只在乎结果。

而人和人的心智，也是自然选择的产物。如果他们的研究能部分解释动物界的博弈策略，恐怕也可以部分应用到人身上。

演化心理学有个很重要的假设，就是人的思维方式不是“全功能通用计算”，不是一个程序处理所有环境。人脑子是有“应用模块”的。当你需要做紧急决策、或者做不太重要的决策时，你往往会调用你“第一反应”的那个应用模块，而不是冷静分析局势、为具体情境开发一个最佳方案——你没这时间精力，很多时候也不值得。“今人乍见孺子将入于井，皆有怵惕恻隐之心。”你需要计算一下这孩子和我是什么关系、我多管闲事会不会耽误我自己的工作、孩子的父母会不会报答我吗？不需要。你调用的感情函数已经帮你处理完了，要做的只是喊出声或者跑过去。

如果一个人遇到任何事情都是靠第一反应，我们可能会说他是“感情用事”。但是没有人能完全抛弃感情。的确，事后看来你这样做出的常常不是最好决策——但是构想一个最好决策也是有代价的啊！这显然不是经济学上那种买个苹果也要花十分钟画效用曲线的“理性人”，但你似乎也不能说这就不“理性”。

而既紧急又不重要的决策，还有比剪子包袱锤更好的例子吗？

所以，从演化博弈论角度来看的话，这个研究并不是真的为了寻找怎么玩剪子包袱锤的办法，而是实验证明了，在我们面对重复博弈时，我们的脑子的内置应用果然像诺瓦克他们模型做出来的那样，有“反思”的倾向；哪怕这博弈只是剪子包袱锤而不涉及囚徒困境。我们没有像一个理性经济人那样计算出剪子包袱锤的纳什均衡是等概率随机出三种手势之一，而是受到我们“本能”的影响——演化留给我们的那个应用模块，这模块也许就是在重复囚徒困境的环境下诞生的。

当然，现在我们既然知道了人的大脑有此倾向，我们就可以针对它设计一套克制策略 (而理性人的纳什均衡就不怕任何克制策略)。我们能意识到自己的“本能”在特定场合下的缺陷，并主动地克服它，这是我们比大部分别的动物厉害的地方。

这很牛逼好吗。这是触及人类思维本质的东西好吗。虽然也许不如阿克斯罗德和诺瓦克那么牛逼但也非常厉害了好吗。

当然，真正的原论文还要更复杂，涉及的层面也更多，而对于囚徒困境的研究也远不止这里讨论的那些。但是我想，这已经足以证明这项研究的意义。不要被标题党欺骗了，如果标题能说明一切，还需要正文干什么呢。

参考文献: Zhijian Wang et al. Social cycling and conditional responses in the Rock-Paper-Scissors game. arXiv:1404.5199 [physics.soc-ph]